Cientistas destacam importância de alto índice de distanciamento social, estratégia universal para achatamento das curvas #AgenciaEscolaUFPR
Por Breno Antunes da Luz, bolsista de Jornalismo
Sob supervisão de Chirlei Kohls
“Certamente o número de infectados seria bem menor se estratégias mais severas de distanciamento social tivessem sido adotadas”, avalia Marcus Beims, pesquisador e professor do Departamento de Física da UFPR. Ele analisou a eficácia das estratégias contra a pandemia ao redor do mundo com outros quatro cientistas da Universidade Federal do Paraná (UFPR), Universidade do Estado de Santa Catarina (Udesc) e Universidade do Estado do Amazonas (UEA). Os pesquisadores avaliaram nove países de três continentes para entender como o combate contra a Covid-19 poderia ser mais positivo. Os resultados reforçam que os melhores métodos são a testagem em massa e o isolamento social enquanto não há vacina disponível para a população.
Os dados foram publicados em dois artigos de revistas científicas internacionais. O mais recente foi disponibilizado online em agosto pela Chaos, Solitons and Fractals, do Reino Unido. Para a análise são revisitados os primeiros resultados publicados na norte-americana Chaos sobre o crescimento do número acumulado confirmado de infectados até o final de março na Alemanha, Brasil, China, Coréia do Sul, Espanha, Estados Unidos, França, Itália e Japão.

Ambas as publicações mostram que estratégias de achatamento das curvas tendem a ser universais, independentemente do país ou continente. “Nosso objetivo é entender a forma de propagação desse vírus e propor estratégias práticas para conter seu crescimento: alto índice de distanciamento social combinado à realização diária de um elevado número de testes e isolamento de infectados”, diz o professor Marcus.
Segundo Eduardo Brugnago, doutorando da UFPR e um dos colaboradores da pesquisa, o estudo produzido se soma com vários outros para evidenciar que a implementação rigorosa de um certo grau de distanciamento social acarreta na redução na quantidade de novos casos. “Medidas de proteção individual reduzem a probabilidade de contaminação. Já outros fatores que mostramos como aliados no enfrentamento à pandemia, como o isolamento efetivo dos infectados, o que requer infraestrutura e logística para realização de testes em massa e alocação segura dessas pessoas, é algo distante de aplicação real no nosso país [por causa do número da população, por exemplo]. Por isso a importância de manter o distanciamento social”.
Além do professor Marcus e do doutorando Eduardo, participaram da pesquisa o professor Rafael da Silva, também do Departamento de Física da UFPR. De outras instituições, integram o grupo os professores César Manchein, da Departamento de Física da Udesc, e Carlos Mendes, da Universidade Estadual do Amazonas.
Modelo matemático
ajustado a dados reais
O estudo foi dividido em duas etapas. A primeira trata dos dados reais, da forma com que o número de casos evoluiu e como essas curvas apresentam comportamento similar para diferentes países. Na segunda parte, os pesquisadores empregaram um modelo matemático com parâmetros ajustados aos dados reais, o que permite traçar cenários futuros hipotéticos.
Os dados reais de análise são usados no modelo chamado Lei de Potência, ao invés da Lei Exponencial comumente usada nesse tipo de pesquisa. Na Lei Exponencial o número de novos casos de infectados dobra a cada intervalo de tempo. Já na Lei de Potência o crescimento é menor e sugere que os modelos utilizados para descrever esse crescimento são diferentes.
“A questão não é tanto o número de infectados, mas sim sobre como ocorre o crescimento. Nesse modelo [Lei de Potência] está incluída a possibilidade de pessoas eventualmente infectarem alguém de um local distante através de uma viagem, por exemplo”, esclarece Marcus.
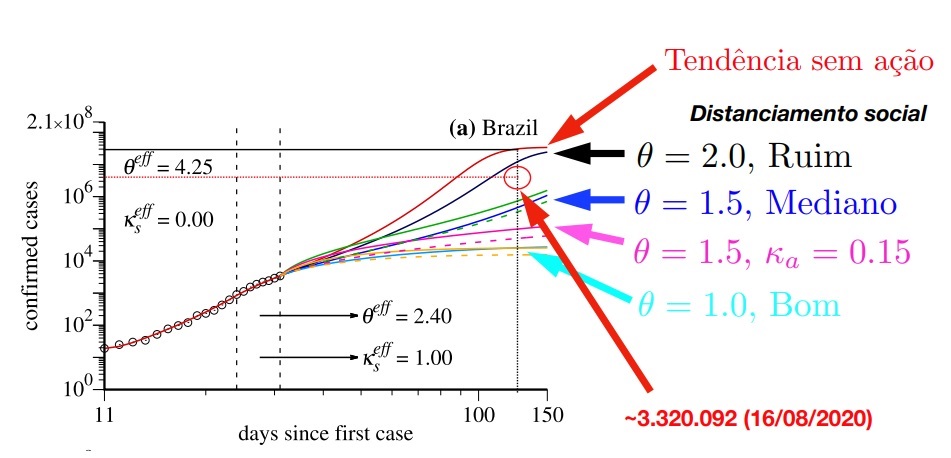
A análise envolve a efetividade da transmissão do vírus e as interações sociais e é similar ao conhecido parâmetro Rt, que diz respeito à média de infectados por um indivíduo durante o período de infecção. Quando o Rt é menor que 1, a propagação do vírus está controlada; quando o Rt é maior que 1, o vírus continua se propagando.
Como medida para simular os testes de assintomáticos, os pesquisadores usaram o parâmetro k_a (kappa). No Brasil, um k_a = 0,15 faria o número de indivíduos infectados diminuir substancialmente, mas ainda não seria suficiente para controlar completamente a propagação do coronavírus. Isso implica testar e isolar diariamente 15% dos indivíduos infectados assintomáticos. “Num país populoso como o Brasil, isso é praticamente impossível, pois para achar tantos indivíduos assintomáticos nesse país imenso precisamos testar muito mais pessoas”, diz Marcus.
Como a contaminação
poderia ter sido menor
O professor Marcus explica que as simulações mostram que se, desde 28 de março, tivéssemos conseguido manter Rt perto de 1, teríamos uma tendência de diminuir em milhões o número de indivíduos infectados no Brasil. “O retorno de atividades nesse momento é péssimo, pois aumenta o Rt fazendo com que o coronavírus possa se espalhar com mais facilidade. Mesmo para cidades onde o número de infectados está diminuindo, o aumento do Rt favorece a infecção de novos indivíduos”.
“O fator mais relevante para conter a pandemia continua sendo o distanciamento social, ou seja, manter o valor de theta (ou Rt) o menor possível”, reforça o pesquisador Marcus.
Novos estudos
O grupo já realiza outras pesquisas específicas para dar sequência ao projeto. Uma delas envolve a evolução do número de casos confirmados de Covid-19 nos estados brasileiros. Outro estudo, em parceria com a Universidade Estadual de Ponta Grossa (UEPG), busca entender a propagação geográfica do vírus no Paraná. A partir disso, os pesquisadores pretendem analisar quais cidades estão mais suscetíveis ao vírus. Além disso, o grupo está realizando pesquisas sobre possíveis efeitos dos dados meteorológicos sobre o número de novos casos do coronavírus.
Clique aqui e leia essa matéria em inglês – a tradução foi feita pelo Centro de Assessoria de Publicação Acadêmica (Capa) da UFPR
Essa reportagem é resultado da ação Banco de Pautas Covid-19, da Agência Escola UFPR












